Génération de terrain et triangulation de Delaunay

La triangulation de Delaunay permet de récupérer une bonne triangulation avec un semis de points. D'un point de vue algorithmique, la triangulation de Delaunay est le problème dual du diagramme de Voronoï. Ceci veut dire que la résolution de l'un entraîne forcément la résolution de l'autre. Nous ne traiterons pas ici la résolution du diagramme de Voronoï. Par contre, cet article tentera de présenter deux algorithmes de triangulation de Delaunay à travers un programme permettant de générer aléatoirement des terrains 3D.

On opèrera en plusieurs temps : il faudra tout d'abord définir les dimensions du terrain, donc ses limites dans un espace tridimensionnel qui seront concrétisées par quatre points symbolisant les quatre coins d'un rectangle et des paramètres d'altitudes, comme une hauteur maximale, afin de donner au plan défini la dimension d'un volume.

On procèdera ensuite à l'insertion systématique de points dans le plan, points qui seront ensuite traités dans l'optique d'un maintien de cohérence de la triangulation de Delaunay.

Lorsque le nombre de triangles considérés sera satisfaisant, l'étape suivante consistera en une mise en place de reliefs via des modifications de hauteurs des points, colorations différentielles selon l'altitude, établissement de niveau de mers.

Bien sûr, comme nous le montrerons ici, la mise en place de la triangulation et la gestion du relief peuvent être faites en même temps. À chaque insertion du point en 2D, nous pouvons affecter la hauteur correspondant à ce point.

Cette partie va présenter globalement les algorithmes sans trop parler de code. Nous allons tenter de rester assez général pour faire passer les idées plus que des lignes de code.

II-A. Initialisation▲

II-B. Triangulation de Delaunay▲

Il existe plusieurs algorithmes qui génèrent, de façon incrémentale, la triangulation de Delaunay. On parle de techniques incrémentales lorsque nous partons d'une triangulation et, en ajoutant un point, nous voulons recalculer les triangles. Pour cet article, nous avons mis en place deux algorithmes : la Destruction-Construction et le Flip Algorithme.

L'algorithme nommé Destruction-Construction est plus facile à aborder, mais compte tenu de sa complexité assez importante en O(n^3), nous avons ajouté l'implémentation du Flip Algorithme qui peut atteindre une complexité de O(n*log(n)) si nous mettons en place un arbre binaire, mais, pour des raisons de temps et de simplifications, nous n'avons pas implémenté l'arbre et donc notre version de l'algorithme atteint des complexités de O(n^2).

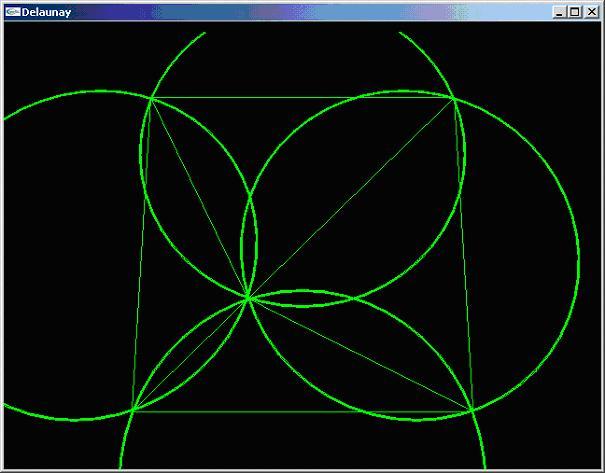
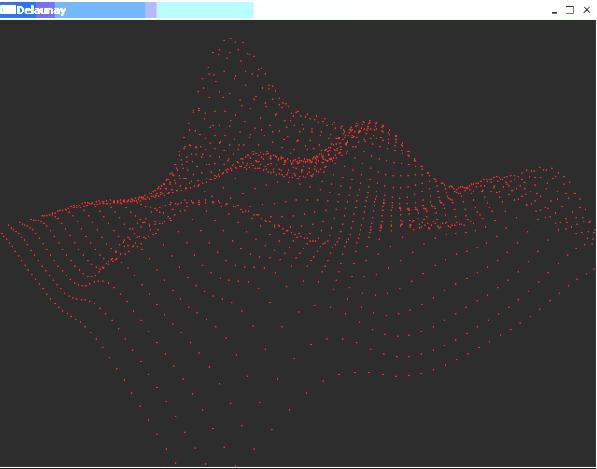
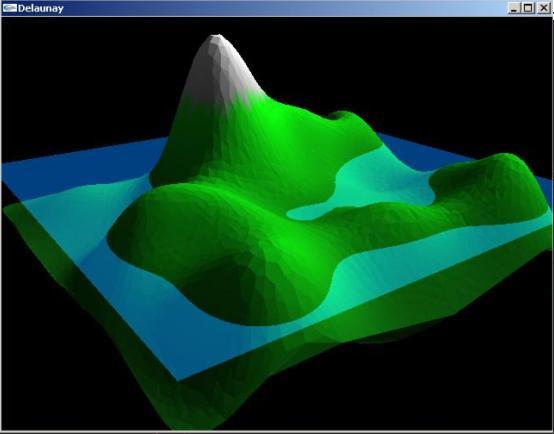
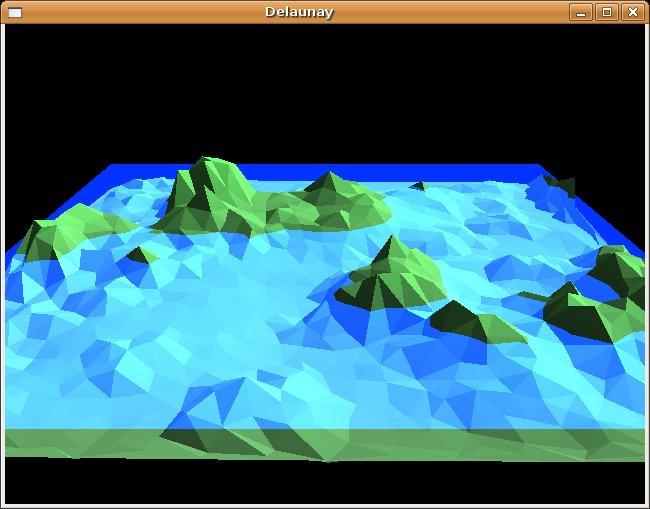
Le code que nous présentons permet de voir la triangulation de Delaunay à l'œuvre et donc de façon 2D ou 3D. La 2D permet de voir le bon fonctionnement de la triangulation et nous avons ajouté la possibilité de voir les cercles circonscrits. En voici, une image :

Un des problèmes dans ces algorithmes est de trouver le triangle dans lequel se trouve le point qui sera ajouté. Nous allons court-circuiter cette recherche en choisissant d'insérer le point dans le triangle qui a la plus grande aire. La position du point est le barycentre des sommets du triangle (éventuellement pondérés). La complexité de la recherche du triangle et du choix du nouveau point se fait donc en O(1) lorsque les listes des triangles sont triées en fonction de leur aire (de façon décroissante pour que le plus grand triangle soit en début de liste).

II-B-1. Triangulation par Destruction/Construction▲

Elle se fait à partir d'une triangulation partielle du semis, et se poursuit par la triangulation existante augmentée d'un point. Donc, partant de quatre points de départ formant deux triangles (donc quatre points déjà triangulés), l'algorithme rajoute des points qui sont intérieurs à la triangulation et qui sont triangulés au fur et à mesure.

On procède ainsi : on utilise un triangle et un point choisi comme indiqué ci-dessus, puis tous les triangles dont le cercle circonscrit contient le point considéré sont détruits. Une fois les triangles illégaux détruits, on construit ceux qui sont engendrés par ce nouveau point, en ajoutant des arêtes reliant au point inséré les extrémités de celles qui n'appartenaient qu'à un seul triangle présent dans la liste de ceux qui ont été supprimés.

On utilise donc principalement deux méthodes : une fonction récursive qui détermine les triangles à éliminer, l'autre les triangles à construire. Voici l'algorithme général en pseudocode :

Algorithme général

Sélectionnez

Fonction inserePoint()
{
//On choisit le plus grand triangle
Triangle t = PremierTriangle();

//Choisir un point dans le triangle
Point p = ChoisirPoint(t);

//Initialiser une liste vide pour la destruction
Liste ld = InitialiseListeVide(),
      lc = InitialiseListeVide();

//On détruit les triangles qui posent problème
detruireTriangles(p,t,ld);

//On construit les triangles
construireTrianges(p,ld,lc);

//On ajoute les triangles
AjouteTriangles(lc,lt);
}

Cet algorithme suit bien le paragraphe précédent. Montrons maintenant l'algorithme de la fonction de destruction :

Destruction des triangles

Sélectionnez

Fonction detruireTriangles(Point p, Triangle t, Liste ld)
{
//Ajoute le triangle t à la liste l
AjouteTriangle(l,t);

//On regarde les triangles voisins
Pour chaque triangle tv voisin de t
  Si le triangle tv n'appartient pas à ld alors
    Si p est inclus dans le cercle circonscrit de tv alors
      detruireTriangles(p,tv,ld)
    FinSi
  FinSi
}

Cette fonction est donc très simple. On ajoute le triangle à la liste des triangles à détruire et on traite chaque voisin. Si le cercle circonscrit d'un triangle voisin inclut le nouveau point, on appelle la fonction récursivement (donc on l'ajoutera à la liste et on regardera ses voisins). Bien sûr, on regarde le cercle circonscrit seulement si le triangle n'appartient pas déjà dans la liste.

Enfin, voici l'algorithme de la fonction de construction.

Construction des triangles

Sélectionnez

Fonction construireTriangles(Point p, Liste ld, Liste lc)
{
Pour chaque triangle t de la liste ld
  Pour chaque voisin tv du triangle t
    Soit p1,p2 les deux points du côté en commun avec t et tv
    nouveaut = CreerTriangle(p,p1,p2)

    //On met a jour l'adjacence entre les triangles tv et nouveaut
    GererAdjacence(tv,nouveaut)

    //Ajouter le triangle nouveaut dans une liste lc
    AjouteTriangle(lc,nouveaut) 
  FinPour
FinPour

//Gerer les adjacences entre les triangles
GererAdjencenceEntreTriangles(lc)
}

Comme vous le voyez, l'algorithme est assez simple. Lorsque vous regarderez le code, la plus grande difficulté est de ne pas se tromper avec les points et les triangles voisins.

II-B-2. Le Flip Algorithme▲

Cet algorithme est plus rapide que le premier puisqu'il a, en principe, moins de travail à faire. C'est une grande fonction récursive (qui pourrait être implémentée en itératif), qui vérifie si les côtés sont légaux. Un côté est défini comme étant l'arête commune à deux triangles. Pour savoir s'il est illégal, nous regardons les points qui ne sont présents que dans un des triangles (donc les points opposés). L'image suivante montre un côté légal entre deux triangles, comme on le voit, les cercles circonscrits ne contiennent pas le point opposé.

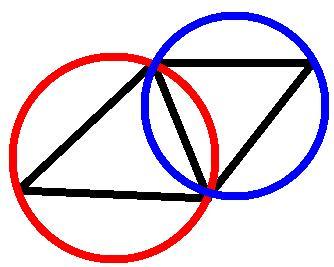
Un côté est considéré comme étant illégal si au moins un de ses deux points est contenu dans le cercle circonscrit du triangle opposé.

Si c'est le cas, le côté illégal est remplacé par un côté relié par les deux points opposés. Et on testera les quatre côtés qui restent pour voir si ce changement a provoqué un autre conflit. L'image qui suit montre un côté illégal et le flip qui permet de rendre ce côté légal :

Donc l'algorithme peut être décrit par :

• insérer le point, détruire le triangle le contenant ;
• créer trois triangles qui ont ce nouveau point comme sommet ;
• vérifier chaque côté externe pour une illégalité.

La vérification des côtés peut être donnée par :

Algorithme de vérification

Sélectionnez

Pour les deux points opposés, vérifier s'ils sont dans le cercle circonscrit du triangle opposé
  Faire
    Si le point est inscrit dans le cercle circonscrit du triangle opposé alors
      Inverser le côté.
      Vérifier les quatre côtés externes pour une illégalité.
    FinSi
  Fin Pour

Comme on voit, c'est donc un algorithme assez facile, mais il faut faire attention à la structure de données que nous utilisons pour l'implémenter. Si on utilise une structure appropriée pour cet algorithme alors le rendu risque d'être plus difficile. De l'autre côté, utiliser une structure idéale pour le rendu risque de rendre l'implémentation de ces algorithmes plus difficile.

Néanmoins, nous avons choisi de favoriser le rendu du terrain puisqu'une fois le terrain créé, nous n'avons plus que le rendu à gérer. Donc l'implémentation de la triangulation sera plus difficile à comprendre et à implémenter.

II-C. Fonctions de reliefs▲

Elles sont de plusieurs types : une première approche consiste à développer un terrain explicite défini par des fonctions exponentielles, donc des régions concaves et convexes selon que l'on souhaite respectivement des vallées ou des montagnes. L'insertion d'un point lui attribue alors la hauteur correspondant à celle du point de mêmes coordonnées sur le plan du terrain explicite. Par opposition à la première approche, qui envisage le terrain de façon globale, une autre manière de procéder serait constituée par des changements apportés localement. Ainsi, une montagne pourrait être définie par son point le plus haut, puis par l'application d'une fonction récursive, une modulation des hauteurs peut être obtenue. On peut de la même manière envisager plusieurs méthodes de modifications des altitudes.

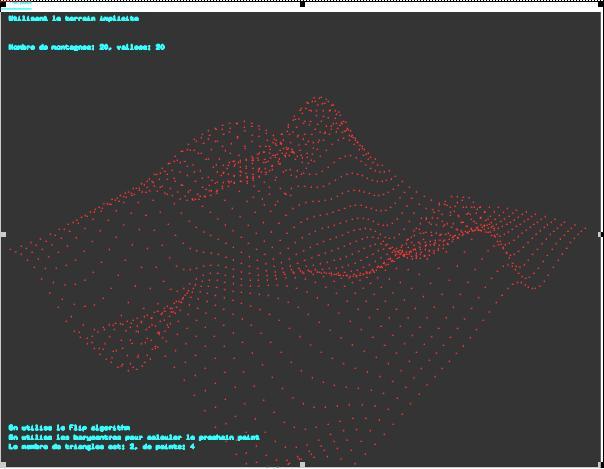
II-C-1. Le terrain explicite▲

Comme le dit l'introduction, l'idée qui gouverne cette méthode est d'essayer d'imiter un terrain lors de la construction des triangles. Ce terrain est défini par un certain nombre de fonctions exponentielles. Nous avons implémenté deux variantes de cette technique.

II-C-1-a. La première méthode▲

La première méthode crée des montagnes et des vallées et l'altitude du terrain est calculée en sommant les valeurs des exponentielles obtenues. Cette méthode donne de bons résultats, mais a l'inconvénient de ne pas toujours affecter tout le terrain, ce qui laisse des morceaux de plaines (ce qui a son charme, mais le contraste est un peu fort). Pour expliquer un peu mieux la génération du terrain, voilà la formule de base d'une des exponentielles:

f(x,y) = (-1)^montagne*hauteur*exp(-etal_x*(x-centre_x)^2-etal_y*(y-centre_y)^2)

Avec :

• montagne est un booléen donnant l'effet concave ou convexe de la courbe ;
• hauteur est la hauteur maximale de l'exponentielle en valeur absolue ;
• etal_x et etal_y sont les degrés d'aplatissement dans chacune des deux directions ;
• (centre_x,centre_y) sont les coordonnées du centre de l'exponentielle, c'est en ces positions que la fonction f atteint son maximum en valeur absolue.

On remarquera que f(centre_x,centre_y) = (-1)^montagne*hauteur (donc la hauteur maximale de la montagne ou minimale de la vallée).

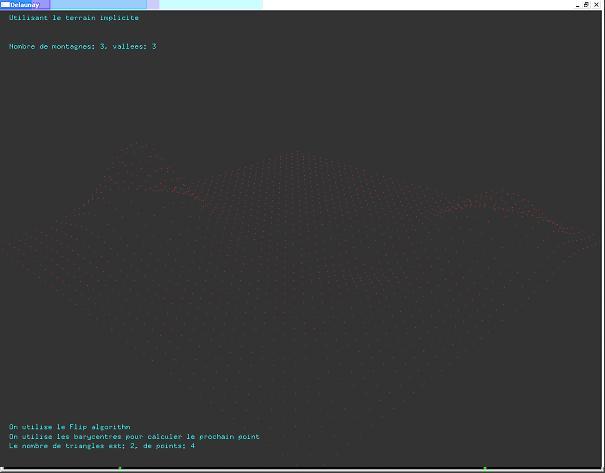
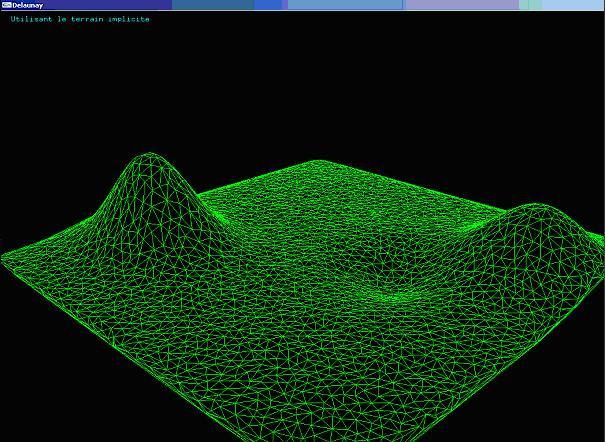
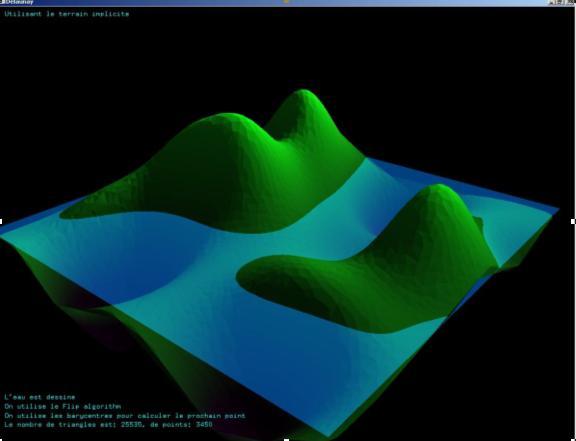
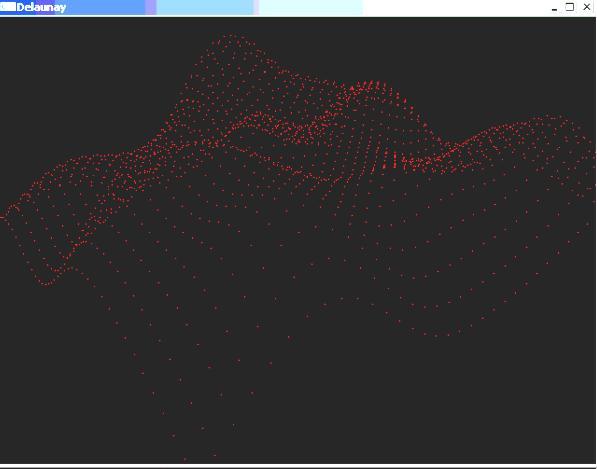
Voici des images montrant le terrain explicite et le terrain obtenu avec un nombre différent de montagnes et vallées.

II-C-1-b. La deuxième méthode▲

Cette variante part du fait qu'il est possible de normaliser le terrain pour l'obliger à se trouver entre une valeur minimale et maximale. Cette méthode n'utilise donc plus l'idée de vallées pour sa création, en fait on utilise que des montagnes. L'idée est de calculer le minimum et le maximum du terrain, la hauteur du terrain est donc donnée par :

 

Sélectionnez

res = haut(x,y)             //calcule de base vu en c.1.a
res = (res-min)/(max-min)   //res sera donc entre 0.0 et 1.0
res = 10*res;               //res sera donc entre 0.0 et 10.0

Il est inutile de dire que cette méthode permet d'avoir autant de montagnes que nous voulons et c'est d'ailleurs préférable. Plus il y a de fonctions impliquées dans le calcul, plus le terrain devient intéressant.

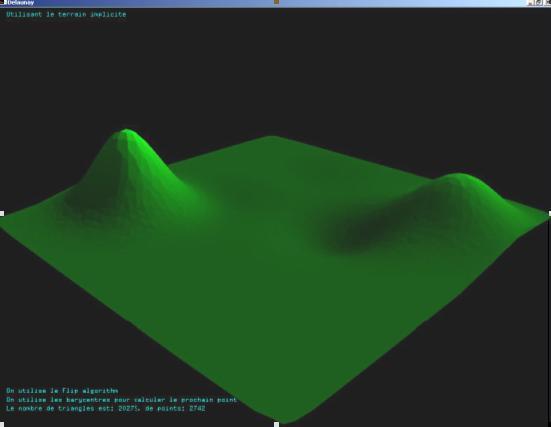
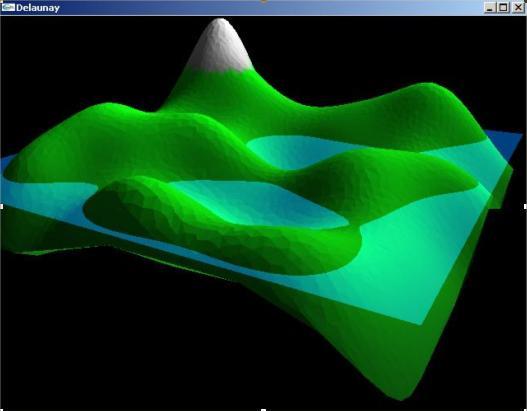
Voici ce que nous obtenons avec cette méthode:

Enfin, nous avons ajouté une petite option qui permet d'accentuer les montagnes et donc d'élargir les parties basses du terrain en ajoutant l'instruction:

 

Sélectionnez

res = haut(x,y)            //calcule de base vu en c.1.a
res = (res-min)/(max-min)  //res sera donc entre 0.0 et 1.0
res = res * res               //res sera donc entre 0.0 et 1.0
res = 10*res;              //res sera donc entre 0.0 et 10.0

C'est la mise au carré qui rend le terrain plus aplati, mais conserve le pic du terrain à 10.

II-C-2. Fonctions locales▲

La conception de ces méthodes suit l'approche décrite précédemment, c'est-à-dire le choix d'un point comme centre d'une montagne suivi de fonctions qui élèvent les points environnants, ce, de manière moindre au fur et à mesure du degré de la récursivité. La hausse d'altitude se propage donc du centre vers la périphérie jusqu'à atteindre soit un nombre d'applications défini, soit une élévation nulle. Il a été ainsi programmé, et ces fonctions ont été conçues avec un certain nombre de paramètres pour pouvoir faire varier leurs résultats : la profondeur de récursivité doit ainsi donner de plus vastes montagnes, la hauteur donnée fera varier l'altitude des pics, le coefficient de réduction, c'est-à-dire la différence d'altitude de deux points juxtaposés, permettra d'étaler les pentes, etc. Un large travail de test et d'observation a été fait afin d'obtenir des résultats variés, mais prévisibles par un paramétrage précis. C'est la raison pour laquelle ce dernier n'est pas implémenté dynamiquement. En effet, pour donner des résultats corrects, les paramètres ont un faible domaine de validité, il a donc été décidé de les garder constants.

Enfin, on distinguera deux manières d'appliquer les fonctions récursives, selon qu'elles puissent ou non s'appliquer plusieurs fois sur le même point. Si c'est le cas, l'élévation étant très importante en début de récursivité, elle s'appliquera plusieurs fois au sommet, entraînant des pics abrupts tandis qu'à la base, les hausses seront faibles, laissant apparaître des pentes douces entre les sommets concernés et ceux qui sont exclus de la montagne. Si c'est le nombre de fois où l'application est faite qui détermine l'arrêt, et si ce nombre est faible, le résultat ressemblera à des massifs de pyramides très pointues auxquels on pourra prêter une apparence minérale. À l'opposé, la fin de récursivité déterminée par une élévation proche de zéro aura pour effet une caractéristique de stalagmite, un pic et une base arrondie. Cette méthode porte le nom de jeun_mont, car si les pentes ne sont pas trop grandes, le relief obtenu ressemble à de jeunes montagnes. L'autre méthode portera donc très logiquement le nom de veil_mont pour des raisons analogues. Il est à noter que, appliqués localement avec de faibles amplitudes, les reliefs conséquents ont l'apparence de massifs rocheux, bien que ces massifs ne ressortiront pas énormément puisque la coloration du terrain est relativement simpliste.

Nous allons présenter ici la plupart des structures qui sont utilisées dans le progamme. Tout d'abord, nous devons expliquer que le programme a, en variable globale, accès aux triangles et aux sommets du terrain. De plus, les sommets et les triangles sont séparés pour une raison d'optimisation de place mémoire. En effet, un sommet étant présent dans plusieurs triangles, si chaque triangle avait la position des sommets directement dans sa structure, cela nécessiterait 3 flottants (ou double) par triangle. Notre système met les points dans un tableau central et les triangles n'ont que les indices des sommets dans ce tableau.

Pour montrer l'efficacité de cette méthode, prenons l'exemple d'un sommet qui se trouve dans deux triangles :

• la première version utiliserait 6 flottants, ce qui représente 6*8 = 48 octets (si c'est des doubles) ;
• la deuxième version utiliserait 3 flottants pour le point et 2 entiers, ce qui revient à 3*8 + 2*4 = 32 octets (si on suppose qu'un double utilise 8 octets et un entier 4) Donc, avec seulement deux triangles pour un sommet, on économise 16 octets.

La structure qui représente notre terrain est donc donnée par :

typedef struct sTabDel
  {
  int nt;                //nbr de triangles, pour info...
  StartT triangles;      //les triangles sont en liste chaînée
  int np;                //nbr de points
  SPoint p[MAX_POINTS];  //les points
  }STabDel;

On a donc un tableau de points et une liste de triangles. La raison d'avoir conservé un tableau pour les points est que nous ne changeons jamais l'ordre des points, nous ne faisons qu'en ajouter et nous n'en supprimons jamais (sauf à la réinitialisation et ceci se fait en mettant simplement np à 0).

Nous ne présenterons pas les structures SPoint (il s'y trouve 3 doubles) où la structure StartT (qui est une structure pour définir une liste chaînée). Par contre, l'élément chaîné STriangle est une structure que nous allons juste le présenter, mais les commentaires devraient suffire pour l'expliquer :

typedef struct sTriangle
  {
  TerranType type;    // Type de terrain du triangle
  bool flip_param;    // Parametre pour le flip
  int p1,p2,p3;       // Indice sur le tableau de sommets dans la structure TabDel
  struct sTriangle *t1,*t2,*t3;      // Pointeurs vers les voisins
  SPoint centre;      // Centre défini comme la structure, mais en 2d donc le z ne sert à rien
  double rayon;       // Rayon du cercle circonscrit au triangle
  double critere;     // Critere pour permettre de choisir un triangle par rapport a un autre (ici l'aire)
  }STriangle, *Triangle;

Une convention existe concernant les triangles t1,t2 et t3 : t1 a comme points communs avec le triangle défini les points p1 et p2, t2 les points p2 et p3, et t3 les points p3 et p1. Bien que cela va compliquer un peu les choses, cette convention est nécessaire pour l'utilisation correcte des algorithmes.

La dernière structure que nous présenterons est la structure qui gère le terrain explicite :

typedef struct sTerrainImpl       //on définit un terrain par un certain nbr de bosses
  {
  int nb_centre;                  //nbr de bosses
  double centre[MAX_CENTER][2];   //les centres
  double etal[MAX_CENTER][2];     //l'etalement
  double hauteur[MAX_CENTER];     //la hauteur
  bool montagne[MAX_CENTER];      //Est-ce une montagne ?

  //juste pour statistiques
  int nb_montagnes;
  }STerrainImpl;

Mais de nouveau, avec les explications données précédemment, la raison des différents éléments de cette structure devrait être claire. La seule chose que nous noterons est la macro MAX_CENTER qui est définie par un define. Nous aurions pu faire une allocation dynamique, mais ceci aurait alourdi le code inutilement, donc nous avons conservé cette macro.

Pour afficher la construction du terrain, nous avons utilisé OpenGL. Nous avons mis en place beaucoup d'options pour faciliter la visualisation du terrain, mais aussi pour jouer avec les différents paramètres. Nous avons mis tous les paramètres en variables globales pour simplifier le code, mais vu leur nombre, ils ont été rassemblés en une structure Param qui est donnée dans le fichier define.h.

IV-A. Les paramètres▲

La triangulation de Delaunay permet d'avoir une bonne triangulation d'un ensemble de points. Le programme présenté ici montre l'implémentation de deux algorithmes qui créent une triangulation de Delaunay, mais aussi qui affiche le terrain en 3D.

Il est aussi à noter qu'un tel projet n'est jamais fini : il sera toujours possible, d'ajouter d'autres objectifs à atteindre, d'autres détails à modéliser, des approches à tester… c'est là la caractéristique d'une modélisation : elle n'est jamais finie, car elle se limite à imiter la réalité qu'elle représente, et donc, tout modèle peut toujours être amélioré, être plus proche de son objet. Une modélisation ne peut être au mieux que satisfaisante.

Jc et Benjamin.

Contenus des fichiers :

Exception faite pour le Define.h tous les fichiers .cpp s'utilisent avec leur fichier .h.

• Le define.h contient toutes les structures de données utilisées plus éventuellement l'une ou l'autre variables globales.
• Delaunay : contient une fonction qui choisit un point et une fonction qui teste si un point se situe dans le cercle circonscrit d'un triangle.
• DestCons.h : contient une fonction qui initialise la structure pour cet algorithme, une fonction pour remettre tout à zéro et la fonction pour recalculer la triangulation (en insérant un point).
• Flipalgo : les fonctions nécessaires au flip algorithme, coté_illégale et l'insertion de points.
• Graphiques : toutes les fonctions impliquant OpenGL.
• Liste : puisque l'on utilise des listes, on a ici toutes les fonctions de base impliquant classiquement celles-ci.
• Main : fonctions utilitaires en plus du programme.
• TerrainExpl : les fonctions pour l'implémentation du terrain explicite.
• Terran : les fonctions de modifications locales.
• Triangle : des fonctions agissant sur les triangles.
• Vecteur : des fonctions agissant sur les vecteurs.

Télécharger cet article en format pdf : pdf (615 kO).

Télécharger la version C du code : zip (27 kO).

Merci à Miles pour ses critiques du code et de l'article, à buchs et à gorgonite pour leur relecture.