Programmation de jeu 2D : Le morpion, Septième partie
Date de publication : 28/06/2006 , Date de mise à jour : 28/06/2006
Par
Jean Christophe Beyler (Autres articles)
Dans ce tutoriel, nous avons présenté dans la partie précédente comment mettre en place une intelligence artificielle. Le problème de l'algorithme Min-Max est sa lenteur, il y a beaucoup d'évaluations inutiles. Dans cette partie, nous allons présenter une optimisation du Min-Max nommée Alpha-Beta.
1. Introduction
2. Présentation de l'Alpha-Beta
2.1. Présentation
2.2. L'algorithme
2.3. Exemple
2.4. Discussion
3. Implémentation
3.1. La fonction calcMin
3.1. La fonction calcIA
3.3. Discussion
3.4. Limitations
4. Remerciements
5. Conclusion
6. Téléchargements
1. Introduction
Le jeu du morpion est un mauvais exemple de la lenteur de l'algorithme Min-Max parce que la fonction d'évaluation est relativement rapide et le nombre de configurations n'est pas énorme.
Mais dès que vous allez tenter de faire tourner l'algorithme Min-Max sur un jeu d'échecs, vous comprendrez le problème. Une solution pour résoudre le problème est de limiter le nombre d'évaluations et de configurations qui seront à parcourir.
Cette partie va donc présenter la variante Alpha-Beta de l'algorithme Min-Max.
2. Présentation de l'Alpha-Beta
Nous allons commencer par présenter l'algorithme. Ensuite, nous présenterons comment modifier les fonctions de la classe IA pour implémenter cette variante.
2.1. Présentation
L'amélioration faite par l'algorithme Alpha-Beta consiste à limiter le nombre de configurations visitées lors du calcul du prochain coup. En effet, il n'est pas toujours nécessaire d'évaluer toutes les configurations.
Pour expliquer comment fonctionne l'algorithme Alpha-Beta, nous allons le faire en présentant rapidement les changements dans les fonctions calcIA, calcMin et calcMax et, ensuite, en montrant le déroulement de l'algorithme sur un exemple. Je pense que ce sera plus clair et plus facile à assimiler.
2.2. L'algorithme
Pour montrer les modifications de l'algorithme Alpha-Beta, nous allons remontrer la version de calcMax :
| Ancien algorithme | Fonction calcMax(Jeu *j, int prof)
{
Soit max = MINIMUM;
Si la partie est terminée ou si la profondeur == 0 alors
retourner eval(n);
Sinon
Pour chaque coup possible
Faire
Jouer le coup
tmp = calcMin(j, prof-1);
Si tmp > max alors
max = tmp;
FinSi
Annuler le coup
FinPour
Retourner max;
} |
Voici la version pour l'Alpha-Beta :
| Nouvel algorithme | Fonction calcMax (Jeu *j, int prof, int alpha, int beta)
{
Soit max = MINIMUM;
Si la partie est terminée ou si la profondeur==0 alors
retourner eval(n);
Sinon
Pour chaque coup possible
Faire
Jouer le coup
alpha = max (alpha, calcIA(j, prof-1, alpha, beta))
Si beta <= alpha alors
retourner alpha
Fin Si
Annuler le coup
Fin Pour
retourner alpha
Fin Si |
Quelle est donc la grande différence? C'est le test dans la boucle qui fait la grande différence. En effet, la partie :
| Différence | Si beta <= alpha alors
retourner alpha
Fin Si |
Ceci permet donc de ne pas étudier toutes les configurations possibles. Pour mieux comprendre les implications de ces ajouts, la prochaine partie montre un exemple concret de parcours d'arbre. Il devrait vous illustrer comment on peut savoir s'il est nécessaire ou non d'étudier un sous-arbre.
2.3. Exemple
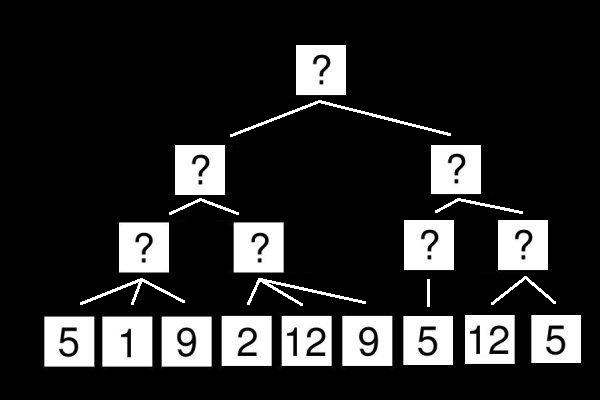
Pourquoi est-ce que ceci fait une si grande différence? Je m'excuse par avance de la longueur de cette sous-section. L'algorithme alpha-beta n'est pas difficile à mettre en place et pas difficile à comprendre lorsqu'on a un exemple. Cet exemple montre le déroulement de l'algorithme en 8 étapes. Voici l'arbre des configurations :
 Arbre de configuration
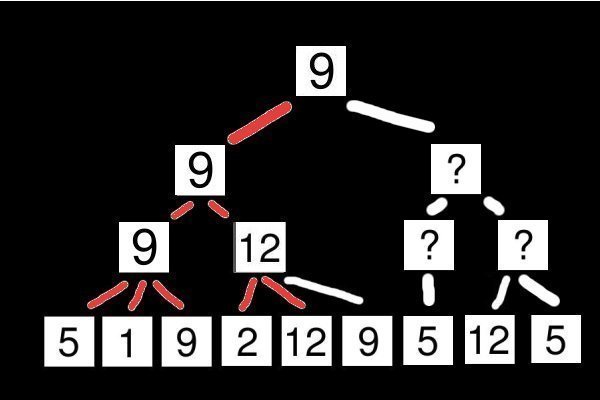
Comme pour l'algorithme du Min-Max, on commence par parcourir l'arbre. Rappelons que la racine de l'arbre est un noeud Max, ses fils sont des noeuds Min et ses petits fils sont des noeuds Max... Regardons l'image suivante :
 Parcours, étape 2
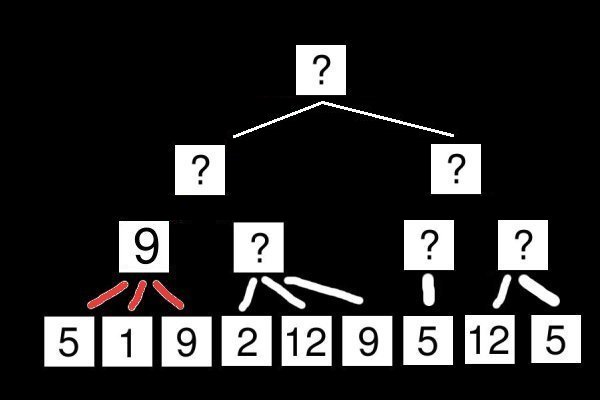
Lors de la première descente, on regarde les trois fils 5, 1 et 9. Etant donné que leur père est un noeud Max, sa valeur devient donc 9. Cette valeur devient donc la valeur intermédiaire de son propre père, c'est ce que montre l'image suivante :
 Parcours, étape 3
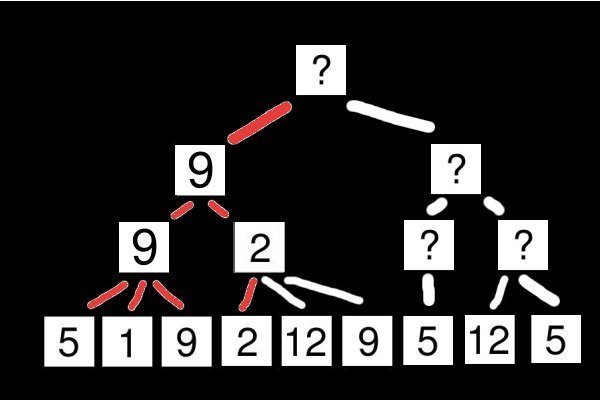
Ensuite, l'algorithme recommence la descente vers les noeuds 2, 12 et 9. Lorsque le noeud 2 est évalué, cette valeur intermédiaire remonte à son père. On le voit ici :
 Parcours, étape 4
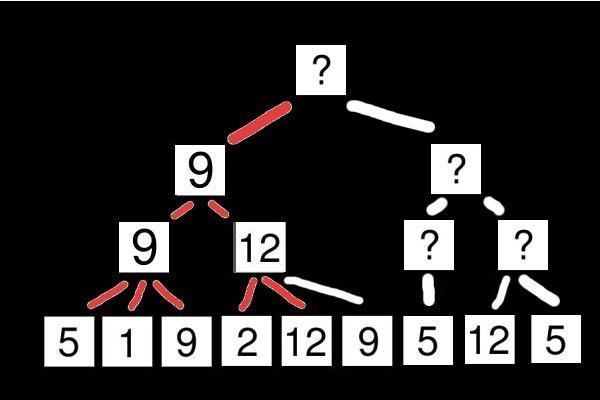
Or lorsqu'on regarde le prochain noeud, la valeur 12 est rencontrée. Etant donné que son père est un noeud Max, il prend la valeur 12 (puisque 12>2).
 Parcours, étape 5
C'est à ce moment que l'algorithme Alpha-Beta réagit différemment que l'algorithme Min-Max. En effet, est-il nécessaire de regarder le troisième fils?
Le petit-fils 12 ne peut que monter. En effet, puisque c'est un noeud max, l'évaluation ne peut que monter. Mais son père est un noeud min, donc pour le moment, il choisira le noeud 9. Donc peu importe l'évolution de la valeur du petit-fils droit, le fils gauche choisira de toute facon le sous-fils gauche. Il est donc inutile de regarder le troisième noeud.
On a donc terminé l'évaluation du sous-arbre gauche. La racine récupère donc la valeur temporaire 9, comme le montre la prochaine image :
 Parcours, étape 6
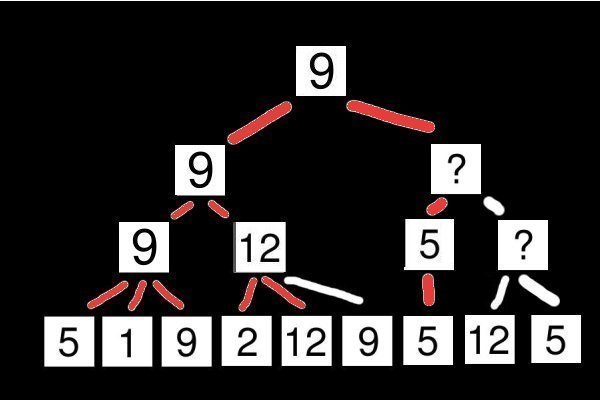
On commence donc l'évaluation du sous-arbre droit. Le premier sous-fils prend la valeur temporaire 5.
 Parcours, étape 7
Donc la valeur remonte au fils droit qui prend cette valeur temporaire, comme le montre cette dernière image :
 Parcours, étape 8
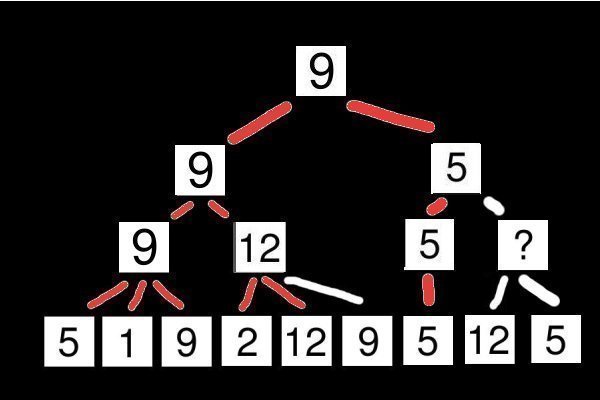
Maintenant est-ce la peine de continuer les évaluations? La réponse est bien sûr non! L'évaluation du fils droit ne peut que descendre (puisque c'est un noeud Min). Donc la racine aura un choix entre l'évaluation 9 du fils gauche et le fils droit qui aura une évaluation forcément plus petite que 5. Puisque la racine est un noeud Max, il prendra donc la valeur 9. Il est donc inutile de regarder les autres noeuds.
2.4. Discussion
Donc finalement, en connaissant quelques valeurs clés, il est possible de savoir si l'évaluation d'un noeud ou même d'un sous-arbre est nécessaire ou pas.
La beauté de l'algorithme Alpha-Beta est sa simplicité pour permettre un tel mécanisme. La suite de cet article va donc montrer ce qui change dans le code.
3. Implémentation
L'implémentation de l'algorithme Alpha-Beta ressemble énormément à celle du Min-Max. On va
commencer par montrer les prototypes des fonctions de la classe IA.
| Prototype des fonctions |
void calcIA(Jeu *j, int prof);
int calcMin(Jeu *j, int prof, int alpha, int beta);
int calcMax(Jeu *j, int prof, int alpha, int beta); |
Remarquez l'ajout des deux paramètres alpha et beta. En rappelant la présentation de la section précédente, l'algorithme de l'Alpha-Beta est exactement le même que celui du Min-Max. Les seules différences sont :
- Nous n'initialisons plus les variables min et max avec des valeurs minimales et maximales. A la place, nous utiliserons les valeurs d'alpha et de beta.
- La variable alpha est mise à jour dans les noeuds max.
- La variable beta est mise à jour dans les noeuds min.
- Nous arrêtons le parcours si la variable alpha se retrouve supérieure à beta.
3.1. La fonction calcMin
Puisque nous avons présenté le code de la fonction calcMax, nous allons montrer le code de la fonction calcMin. Je ne vais pas mettre tout le code puisque le début du code est exactement le même que l'algorithme Min-Max.
| Modification de la fonction calcMin | for(i=0;i<3; i++)
for(j=0;j<3;j++)
{
if(jeu->estVide(i,j))
{
jeu->joue(i,j);
tmp = calcMin(jeu, prof-1,alpha,beta);
jeu->annuleCoup(i,j);
if(alpha<tmp)
{
alpha = tmp;
}
if(beta <= alpha)
{
return alpha;
}
}
}
return alpha; |
Si vous faites une comparaison avec la version de l'algorithme Min-Max, on ne fait qu'ajouter deux tests. La mise à jour de la variable alpha se fait comme la variable max de la version Min-Max. La grande différence est l'ajout du deuxième test qui permet de sortir du parcours des configurations. Si beta devient inférieur à la variable alpha, on sait qu'on peut sortir de la fonction.
3.1. La fonction calcIA
La seule nouveauté de la fonction calcIA de la version Alpha-Beta se retrouve dans le corps du nid de boucles. Voici les différences :
| Nouveauté dans la fonction calcIA |
tmp = calcMin(jeu, prof-1,alpha,beta);
if(alpha<tmp)
{
alpha = tmp;
maxi = i;
maxj = j;
} |
Donc finalement, la seule différence est de passer la valeur de la variable alpha à la fonction calcMin. Ceci permet de réduire le nombre de configurations étudiées.
3.3. Discussion
Voilà, c'est tout! Je me doute que cela semble un peu magique. Il suffit de relire la deuxième section pour comprendre le principe et revoir cette section pour bien regarder comment l'ajout de ces quelques instructions permet de limiter le nombre de configurations.
Enfin, je pensais que ce serait intéressant de regarder le nombre de configurations étudiées lors du premier coup (l'IA jouera donc le premier coup) :
| Niveau de l'IA |
Min-Max |
Alpha-Beta |
| IA Facile : |
504 |
125 |
| IA Moyen : |
15120 |
1985 |
| IA Difficile : |
255168 |
8453 |
Je pense que le tableau montre bien l'intérêt de l'algorithme Alpha-Beta.
3.4. Limitations
A cause de la spécificité de l'algorithme Alpha-Beta, nous ne pouvons plus utiliser l'amélioration de l'algorithme Min-Max pour avoir un jeu plus aléatoire. Rappelons cette modification :
| Modification de l'algorithme | if((tmp>max)||((tmp==max)&&(Rand::randi(2)))) |
Ceci permet de choisir un coup parmi d'autres de la même valeur. Le problème dans l'algorithme Alpha-Beta est que ceci n'est plus possible puisque le retour des fonctions calcMin et calcMax n'est plus vraiment la valeur de l'évaluation du fils. Ce n'est donc pas forcément l'évaluation du noeud mais le retour de la valeur alpha ou beta.
La seule solution pour permettre de remettre cette possibilité d'aléatoire est d'enlever cette gestion de la valeur alpha et donc de perdre un peu l'efficacité de l'algorithme.
Voici donc le nouveau code de la fonction calcIA :
| Nouveau code Alpha-Beta |
if(max<tmp)
{
max = tmp;
maxi = i;
maxj = j;
} |
Donc finalement le code ressemble plus à la version Min-Max (honnêtement, c'est le code du Min-Max, à part le passage des variables alpha et beta à la fonction calcMax). Nous pouvons montrer le tableau qui compare les deux versions :
| Niveau de l'IA |
Nouveau Alpha-Beta |
Alpha-Beta de Base |
| IA Facile : |
227 |
125 |
| IA Moyen : |
2973 |
1985 |
| IA Difficile : |
14113 |
8453 |
Ce tableau confirme donc qu'on perd un peu de performances avec cette nouvelle méthode, mais on gagne en aléatoire.
4. Remerciements
Et bien sûr, je remercie ma femme qui me laisse tapoter sur le clavier presque tous les soirs!
5. Conclusion
Une petite partie qui clôture finalement ce programme de morpion. En effet, lorsqu'on met en place un algorithme d'intelligence artificielle, on n'a pas un grand pas à faire pour arriver à l'algorithme de l'Alpha-Beta.
Par contre, on voit facilement que c'est un grand avantage de le mettre en place. Cette optimisation permet d'avoir de bonnes performances.
Enfin, ceci finit ce tutoriel sur le morpion. A partir d'un des jeux les plus faciles à faire, on a tout de même fait un grand parcours. Nous avons un système de menu, une gestion d'objet basique, une gestion de la souris et du clavier et une intelligence artificielle.
J'espére que vous avez apprécié cette série, qu'elle vous a plu et que vous avez appris quelque chose. C'était un plaisir de les faire!
Jc
Liens
6. Téléchargements
 
|
